MBAファイナンス⑥：時間的価値の計算

年利7.5%で複利運用できると仮定して、今後25年間毎年5,000ドルずつ受け取りたい場合（受け取りは年度末）には、本日時点で何ドルを持っている必要があるでしょうか？

この場合、今後25年間毎年発生する5,000ドルを現在価値に割り引くことで求めることができます。

PV = 5,000/(1.075) + 5,000/(1.075)^2 + ….. + 5,000/(1.075)^24 + 5,000/(1.075)^25

= 55,735ドル

つまり、今後25年間5,000ドルずつ受け取るには55,735ドルの貯金が必要となります。

試験などで現在価値を求める場合は、下図のようなタイムラインで直線をひくことをおすすめします。それぞれの時点における必要な金額を確実に求めることが可能になります。

例題：

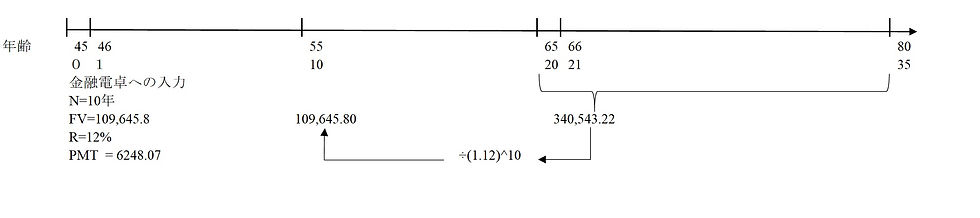
あなたは現在45歳です。あなたは55歳になるまでの10年間で貯金することを決意しました。貯金する目的は、65歳から80歳までの15年間で毎年50,000ドル受け取れるようにすることです。あなたの貯金に対する運用利回りを12％と仮定したとき、今後10年間で毎年いくらずつ貯金すればよいでしょうか？　（この問題を解くにはエクセル又は金融電卓が必要になります。）

65歳から80歳まで毎年50,000ドル受け取る年金の65歳時点での将来価値：340,543ドル

上記の金額を55歳時点まで割り引いた時の将来価値 = 340,543 / (1.12)^10 = 109,645ドル

10年後の将来価値109,645ドルの為に、今後積み立てるべき金額 = 6,248ドル

将来にわたって永遠の利払いが約束された債券がある場合、その金額はどうなるでしょうか？

その債券の価格（現在価値）は、毎期の利払いの金額Cと利回りr の関係から下記の通り表記することができます。

PV = C / r

つまり、毎年250ドルの支払いが約束されている債券の現在の価格は

PV = 250 / 0.08 = 3,125ドル　となります。

投資を行う際に、その投資がどのくらい魅力的かを判断するためのルールとして「72のルール」というものがあります。

利回りが r %で複利運用した時、当初の投資金額が倍になるまでかかる年数は概ね72/r年であるというものです。

つまり、利回りが2％の時、当初の投資金額が倍になるまでには72 / 2 = 36年を要することになります。

また、利回りが10%の時、当初の投資金額が倍になるまでには 72 / 10 ≒ 7 年が必要になります。

いままでの事例では、利払いが年度末に1回のみのケースを想定してきました。

例えば、利回りが8%で100ドル投資して2年間複利運用をした場合、

2年後には　100 × 1.08 × 1.08 = 116.64ドルを得ることになります。

一方で、4％の利息が半年ごとに支払われる場合はどうなるでしょう。

100 × 1.08 × 1.08 × 1.08 × 1.08 = 116.99ドルが2年後に得られることになります。

年1回の支払いの場合よりも、6カ月前に支払われた分の金利に対しても利息がつくためより多くの金額を得られることになります。

もし、利払いが年1回とすると　100 × (1 + 0.08/12)^24 =117.29 となります。

同じ利回り8%でも、利払いの回数が年間何回かによって実効利子率は異なるということになります。

なお、利回りr と実効利子率の関係を表すと下記の計算式となります。

実効利子率 ＝ ( 1 + r/k)^k - 1

利回りが8%で100ドル投資した場合の、利払回数と合計受け取り額の関係は下記の図の通りとなります。

利払いの回数が1回から2回になることの実効利子率への影響は相対的に大きいですが、ある水準を超えるとそこまで影響がないことがわかります。

一般的に、利息は名目利子率で表現されますが、あなたの財産に対する実質的な影響を考慮する場合、実質利子率によって評価する必要があります。

あなたが10％の利率で100ドルを銀行口座に預けたとします。インフレ率が8％、12％の時、当初預けた100ドルはどれほどの購買力を持つことになるでしょうか?

（もちろん、日本でこんな高い利回りを銀行の利息に望むことはできませんが、計算しやすいように10％の利率と仮定しています。）

10％の名目利子率ですので、一年後あなたは100 × 1.1 = 110ドルを受け取ることになります。

もし、インフレ率が8％の場合、1年後の110ドルは8%分その価値を失うことになります。つまり、現在との比較で、1年後の110ドルは110 / (1.08) = 101.85ドル分の購買力を持つことになります。 つまり、1.85% は実質利子率となります。

一方で、インフレ率が12％の時はどうでしょうか? インフレ率が12％の場合、1年後の110ドルは812%分その価値を失うことになります。つまり、現在との比較で、1年後の110ドルは110 / (1.12) = 98.21ドル分の購買力を持つことになります。 つまり、-1.79% が実質利子率となります。

実効利子率と名目利子率、インフレ率の関係は以下のような関係で示すことができます。

( 1 + 名目利子率) / ( 1+ インフレ率) – 1 = 実効利子率

※ 概算を計算したいということであれば、(名目利子率 - インフレ率 ) で実行利子率を求めることは可能です。

次の記事：第07回

前の記事：第05回

目次：MBAファイナンス